Реcемплинг II. Сравнение работы цифровых и аналоговых фильтров высоких порядков в тракте звука и ответы на вопросы
Содержание
Внимание — эта публикация является уточнением первой части статьи[1] и ответом на вопросы из комментариев к ней. Для понимания о чём в ней идёт речь, необходимо ознакомиться с предыдущей[2] если вы этого ещё это не сделали.
Среди многочисленных комментариев к моей последней статье были два очень характерных вопроса — от группы людей, которых я условно могу отнести к категории “практиков”, и человека, который, возможно сам того не желая, озвучил позицию близкою многим аудиофилам.
Мне стало ясно, что далеко не всем понятны объяснения, основанные на теории спектрального разложения сигнала и дальнейшей манипуляцией с гармониками. Ниже я сделал попытку осветить отдельные вопросы из предыдущей статьи ещё более наглядно.
Итак, под катом рассмотрим две темы:
Почему цифровые фильтры в трактах обработки звука не всегда зло
Почему аналоговые фильтры высокого порядка сложно реализовать в серийных устройствах
Попробую раскрыть обе эти заслуживающие внимания темы как можно более доступным языком.
Почему цифровые фильтры в трактах обработки звука не всегда зло
Вопрос первый от FreeMind2000[5]:
Просветите не специалиста? 😉
Первоначальная цепочка такая:
1) Живой звук -> АЦП(16бит, 44.1 КГц) -> CD
2) CD -> 16бит -> Микроконтроллер -> ЦАП(16бит, 44.1 КГц) -> восстановленный звукПосле апгрейда:
2) CD -> 16бит -> Микроконтроллер + (Некий фильтр преобразующий 16бит в 18, 44.1 КГц в 44.1*4) -> ЦАП(18бит, 44.1*4 КГц) -> восстановленный звукТ.е. в апгрейде мы всего лишь:
1. Поставили более дорогой ЦАП (с повышенной частотой дискретизации и разрядностью)
2. За счет придумывания(интерполирования) отсутствующих семплов на шкале времени CD — увеличили кол-во воспроизводимых семплов.
Верно?Тогда, внимание, вопрос:
1. А действительно ли мы улучшили качество звука, добавив семплы, которые в оригинале (живом звуке) могли отличаться от тех, которые мы придумали(интерполировали)? Ведь, то что мы записали с частотой 44.1 КГц — было реально зафиксировано микрофоном, а то что было между записанными семплами нам не известно.2. На сколько далеко наша фантазия (прошу прощения, интерполяция 🙂 может нас завести? Т.е. теоретически, мы можем интерполировать и 8битный звук и 4х…
3. И о каком таком повышении качества мы говорим?
Для человека средний порог частоты воспринимаемого звука 20 кГц, мы воспроизводим с частотой 44.1 КГц — есть ли смысл в дальнейшем увеличении?.. Повышение точности воспроизведения на 2 разряда — единственное, что имеет отношение к реальному улучшению качества, хорошо, а кто-нибудь знает сколько разрядов может различать человеческое ухо? 😉
Да, теорема Найквиста верна, но если даже по двум точкам можно восстановить частоту периодического что немаловажно сигнала, то это не значит что это с успехом может сделать DAC, особенно без применения фильтров! Тем более это касается сложного сигнала, представляющего из себя суперпозицию большого числа гармоник, порой резко появляющихся и исчезающих или меняющих тон.
Для того, чтобы проникнуть в суть проблемы необходимо понять следующее — совершив акт операции оцифровки мы тем самым невозвратно исказили сигнал. Даже если использовали идеальный микрофон, усилитель и аналого-цифровой преобразователь.
Давайте для наглядности перейдём от теории к практике и изобразим форму исходного сигнала на фоне сигнала, выходящего с идеального DAC.
Напомню, что DAC или по русски ЦАП через равные промежутки времени извлекает оцифрованное значение и фиксирует его на своём выходе. В результате мы получаем ступенчатый сигнал. На нашем рисунке минимальный шаг по вертикали и горизонтали равен одной клеточке. За ширину ступенек отвечает частота оцифровки, а дискретность по вертикали определяется разрядностью АЦП. Как от неё зависит качество оцифрованных сигналов видно на примере оцифровки второго бита. Реальное значение лежит практически посередине между двумя допустимыми целочисленными значениями, которое может присвоить сэмплу АЦП. Оно выбрало нижнее, и мы получили весьма большую ошибку. Надеюсь, теперь всем понятно почему даже в идеальном АЦП младший разряд нельзя считать значащим.

Посмотрим что же делает наша микросхема от SONY. Она в увеличила частоту сэмплирования в 4 раза. Мало того, она ещё и по вертикали добавила разрешения за счёт того, что увеличила разрядность сигнала с 16 до 18 бит. Далее, с помощью фильтра производится аппроксимация сигнала и вставляются три промежуточные точки, причём точность их установки выше как по горизонтали так и по вертикали в 4 раза, чем до сделанных преобразований. Аккуратной расстановкой этих точек занимается фильтр. Чем выше его порядок, тем качественнее он производит аппроксимацию.
Однако, после выполнения этих операций мы всё равно имеем ступенчатую структуру, не изображённую на рисунке — вместо них я изобразил жирные точки на трёх первых сэмплах. И тут уже в дело вступает простейший фильтр низкой частоты второго-третьего порядка, который сглаживает эти ступеньки. Результат показан ниже:

Здесь карандашная кривая — исходный сигнал.
Красная кривая — сигнал на выходе 16 битного ЦАПа.
Зелёный участок кривой — то что мы получили после операции ресемплинга и последующего применения простейшего фильтра.
Надеюсь, что FreeMind2000 и его сторонники согласятся, что “чистый неискажённый ступенчатый звук с выхода ЦАП” выглядит меньше похожим на оригинал, чем исковерканный цифровыми извращениями?
Замечу, что первое слева колебание имеет основную гармонику где-то в районе 44/7=6 килогерц, при этом на вид весьма сильно искажается при оцифровке с частотой 44 КГц. Представляете насколько будет похожим на оригинал сигнал с частотой в 17 килогерц?
Тут важно отметить то, что цифровые фильтры при желании могут не тронуть опорных точек полученных с 16 битного ЦАП — лишь расставить между ними вспомогательные, сглаживая кривую по своему усмотрению.
В силу ряда причин, это невозможно сделать применяя вместо цифры аналоговые фильтры высоких порядков. Тут кстати самое время перейти к вопросу вернее утверждению, высказанному AntonSor и горячо поддержанному dernuss[6][7][8]
Почему аналоговые фильтры высокого порядка сложно реализовать в серийных устройствах
Tекст комментария AntonSor:
[9]
Для того, чтобы обрезать все, что лежит за границами звукового диапазона (20 кГц) и получить затухание под 40 дБ на 44 кГц, да с ровной фазовой характеристикой, требуется (с ровной — это фильтр Баттерворта) фильтр 7 порядка, это три операционных усилителя и по 10 5%-е резисторов и конденсаторов на канал. Да, громоздко, но не невозможно. Два счетверенных операционных усилителя типа TL074. В любительском приемнике прямого преобразования бывает больше (в фазовращателе).
Чтобы не заниматься все праздники ликбезом, я лишь вскользь упомяну, что качественные фильтры высокого порядка невозможно построить на операционных усилителях общего применения, к которым относятся TL074 от TI.
Совсем немаловажно, что аналоговые фильтры низкой частоты высоких порядков порождают серьёзные фазовые искажения, особенно в районе частоты среза. Доказывать эту общеизвестную истину чередой длинных формул нашим глубокоуважаемым товарищам я также не стану, лишь приведу картинку из одной моей прошлой статьи[10], которая показывает как жестого фазовые искажения обходятся с формой сигнала.
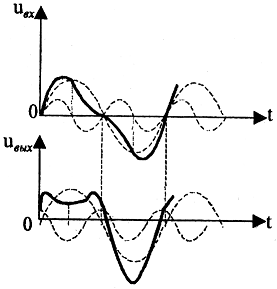
А в заключении по просьбе трудящихся остановлюсь на причине, по которой без точно подобранных номиналов деталей, фильтры высокого порядка не будут давать красивых идеальных расчетных характиристик, как на нижеприведённой нормированной по частоте зависимости ослабления сигнала от порядка фильтра Баттерфорта в логарифмических координатах.
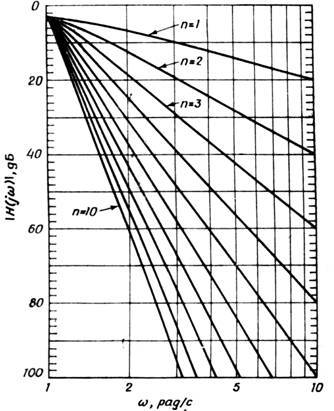
Для того, чтобы построить фильтр, приближающийся по этому параметру к цифровому, описанному в прошлой статье, необходим восьмой — десятый порядок.
Ниже показаны передаточная функция идеального ФНЧ и фильтров Баттерфорта разных порядков.
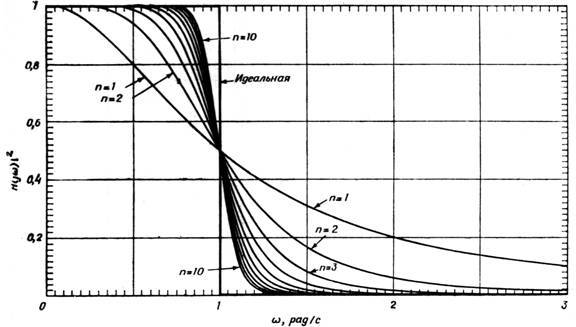
Каким образом обычно строятся подобные фильтры? Очень просто — берётся ФНЧ второго порядка построенный, например, по приведённой ниже схеме…
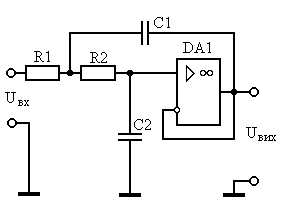
Отлично, давайте посмотрим на график, который показывает как меняются параметры фильтра Баттерворта второго порядка обратите внимание что по горизонтали отложен линейный масштаб от разброса номиналов компонентов в цепи обратной связи.
А теперь представим себе суперпозицию передаточных характеристик нескольких таких звеньев с разными частотами среза, обусловленных разбросом компонентов.

Нетрудно догадаться, что мы не получим в результате эффекта повышения крутизны фильтра в зависимости от порядка. В дополнение мы породим лишние горбы на характеристике, которые станут причиной интермодуляционных искажений.
На самом деле ситуация ещё хуже потому, что разброс влияет не только на частоту среза, но и на другие параметры каждого из звеньев. Полученный в результате отфильтрованный звук в исполнении рака, лебедя и щуки возможно годится по качеству для динамика на выходе регенеративного приёмника, но попытка применить его в высококачественном DAC ничего кроме нездорового смеха у потенциальных покупателей не вызовет.
P.S. Не смог удержаться от использования в загаловке фрагмента рисунка из прекрасного комментария к первой части от пользователя Refridgerator[11]
Использованны источники
- ^ первой части статьи (geektimes.ru)
- ^ предыдущей (geektimes.ru)
- ^ Почему цифровые фильтры в трактах обработки звука не всегда зло (geektimes.ru)
- ^ Почему аналоговые фильтры высокого порядка сложно реализовать в серийных устройствах (geektimes.ru)
- ^ FreeMind2000 (geektimes.ru)
- ^ FreeMind2000 (geektimes.ru)
- ^ AntonSor (geektimes.ru)
- ^ dernuss (geektimes.ru)
- ^ AntonSor (geektimes.ru)
- ^ одной моей прошлой статьи (geektimes.ru)
- ^ Refridgerator (geektimes.ru)













